| This algebra-related article is a stub. You can help Wikipedia by expanding it. |
In ancient Indian mathematics, a Vedic square is a variation on a typical 9 × 9 multiplication table. The entry in each cell is the digital root of the product of the column and row headings i.e. the remainder when the product of the row and column headings is divided by 9 (with remainder 0 represented by 9).
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 2 | 2 | 4 | 6 | 8 | 1 | 3 | 5 | 7 | 9 |
| 3 | 3 | 6 | 9 | 3 | 6 | 9 | 3 | 6 | 9 |
| 4 | 4 | 8 | 3 | 7 | 2 | 6 | 1 | 5 | 9 |
| 5 | 5 | 1 | 6 | 2 | 7 | 3 | 8 | 4 | 9 |
| 6 | 6 | 3 | 9 | 6 | 3 | 9 | 6 | 3 | 9 |
| 7 | 7 | 5 | 3 | 1 | 8 | 6 | 4 | 2 | 9 |
| 8 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 9 |
| 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 |

Numerous geometric patterns and symmetries can be observed in a Vedic square some of which can be found in traditional Islamic art (Pritchard, 2003).
[edit] Algebraic Properties
If we ignore the ninth column and the ninth row, (which are all nines) we are left with the semigroup 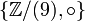 where
where  is the set of positive integers partitioned by the residue classes modulo nine. Also, the operator
is the set of positive integers partitioned by the residue classes modulo nine. Also, the operator  means the abstract "multiplication" between the elements of this semigroup. If {a,b} are elements of
means the abstract "multiplication" between the elements of this semigroup. If {a,b} are elements of 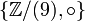 then
then  can be seen as,
can be seen as,  .
.
This does not form a group since not every non-zero element has a corresponding inverse element, for example  but there is no
but there is no 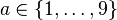 such that
such that 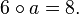 . That is because 9 is not a prime number: 3 and 6 which are not co-prime to 9 do not fall within the multiplicative group of integers modulo 9.
. That is because 9 is not a prime number: 3 and 6 which are not co-prime to 9 do not fall within the multiplicative group of integers modulo 9.
[edit] See also
[edit] References
- Deskins, W.E. (1996). Abstract Algebra. New York: Dover. pp. 162–167. ISBN 0486688887.
- Pritchard, Chris (2003). The Changing Shape of Geometry: Celebrating a Century of Geometry and Geometry Teaching. Great Britain: Cambridge University Press. ISBN 0521531624.
No hay comentarios:
Publicar un comentario
yesyukan